|
|
@@ -23,9 +23,9 @@
|
|
|
|
|
|
## 1.旋转矩阵
|
|
|
|
|
|
-关于旋转矩阵我们在前几节教程中已经介绍了,旋转矩阵采用的是`旋转后的坐标系`三个轴分别与`原坐标系`三个轴的夹角余弦值共九个数字组成3*3的矩阵。
|
|
|
+关于旋转矩阵我们在前几节教程中已经介绍了,旋转矩阵采用的是`旋转后的坐标系`三个轴分别与`原坐标系`三个轴的夹角余弦值共九个数字组成的3*3矩阵。
|
|
|
|
|
|
-旋转矩阵一般记作记作$R$
|
|
|
+旋转矩阵一般记作$R$
|
|
|
|
|
|
> 若两个坐标系姿态相同,其旋转矩阵为单位矩阵。
|
|
|
|
|
|
@@ -34,14 +34,14 @@
|
|
|
|
|
|
|
|
|
|
|
|
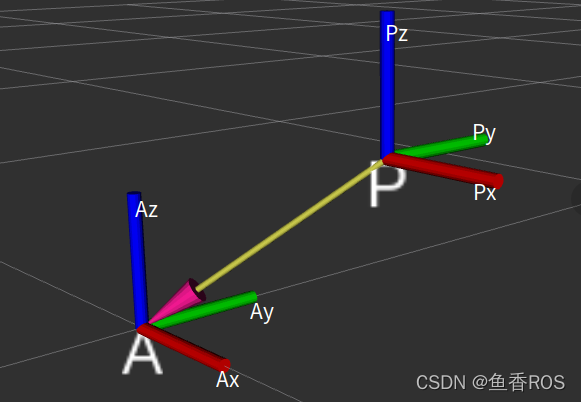
-如图,描述`坐标系{P}`和`参考坐标系{A}`之间的姿态关系来表示${^A_P}R$点的姿态。
|
|
|
+如图,描述`坐标系{P}`和`参考坐标系{A}`之间的姿态关系的旋转矩阵用符号${^A_P}R$来表示。
|
|
|
|
|
|
|
|
|
$$
|
|
|
{^A_P}R=[{^A}x_{P} \ {^A}y_{P} \ {^A}z_{P}] = \begin{bmatrix}{r_{11}}&{r_{12}}&{r_{13}}\\{r_{21}}&{r_{22}}&{r_{23}}\\{r_{31}}&{r_{32}}&{r_{33}}\\\end{bmatrix} \tag{旋转矩阵}
|
|
|
$$
|
|
|
|
|
|
-两个向量的点乘=两个向量的长度(1)与它们夹角余弦的积,所以$r11$可以表示为向量$P_{x}$与$A_{x}$的点积,旋转矩阵就可以写为下面的形式
|
|
|
+两个向量的点乘=两个向量的长度(1)与它们夹角余弦的积,所以$r11$可以表示为向量$P_{x}$与$A_{x}$的点积,旋转矩阵就可以写为下面的形式
|
|
|
|
|
|
$$
|
|
|
{^A_P}R = \begin{bmatrix}
|
|
|
@@ -52,7 +52,7 @@ $$
|
|
|
$$
|
|
|
|
|
|
|
|
|
-### 1.2 绕某一轴旋转$\theta$转旋转矩阵
|
|
|
+### 1.2 绕某一轴旋转$\theta$角的旋转矩阵
|
|
|
|
|
|
`新的坐标系`绕`原坐标系`某一坐标轴旋转任意角度得到的旋转矩阵有如下等式。
|
|
|
|
|
|
@@ -88,9 +88,9 @@ $$
|
|
|
## 2.欧拉角-绕坐标轴的旋转
|
|
|
|
|
|
### 2.1 12种旋转顺序
|
|
|
-旋转矩阵是一个冗余的(九个值之间存在约束关系),可以只需要三个参数来表示旋转矩阵。聪明的鱼粉肯定会想到,假如知道坐标系绕分别绕X、Y、Z轴的旋转角度,不就同样可以表示旋转了吗?
|
|
|
+旋转矩阵是一个冗余的(九个值之间存在约束关系),可以只需要三个参数来表示的矩阵。聪明的鱼粉肯定会想到,假如知道坐标系绕分别绕X、Y、Z轴的旋转角度,不就同样可以表示旋转了吗?
|
|
|
|
|
|
-这个猜想是对的,结合1.2中的绕三个轴的旋转的三个$\theta$,按照特定的顺序将对应的旋转矩阵乘起来就可以确定一个旋转矩阵。
|
|
|
+这个猜想是对的,结合1.2中绕三个轴旋转的三个$\theta$,按照特定的顺序将对应的旋转矩阵乘起来就可以确定一个旋转矩阵。
|
|
|
|
|
|
但需要注意的是,矩阵的乘法不具备交换性,所以旋转顺序不同会造成不同的结果。
|
|
|
|
|
|
@@ -156,19 +156,19 @@ $$
|
|
|
- 接着坐标系{B}绕着A的y轴`Ay`旋转$\beta$
|
|
|
- 接着绕`Az`旋转$\gamma$
|
|
|
|
|
|
-上述三次旋转中,旋转时都是绕着A坐标系的xyz轴为参考坐标系,该旋转方式成为固定旋转轴的旋转,称之为固定角欧拉角或固定轴旋转。
|
|
|
+上述三次旋转,都是以A坐标系的xyz轴为参考坐标系进行旋转,该旋转方式为固定旋转轴的旋转,通常称之为固定角欧拉角或固定轴旋转。
|
|
|
|
|
|
#### 2.2.2 参考自身坐标系
|
|
|

|
|
|
|
|
|
我们也可以不沿着坐标系A的各轴旋转,而是绕旋转之后B的某一轴再次旋转,我们称之为非固定旋转轴的欧拉角。
|
|
|
|
|
|
-> 小鱼说:无论是参考自身坐标系还是参考固定的坐标系,都有12种旋转方式,所以欧拉角有12*2=24种旋转方式,后面的计算中我们也直观的感受到24种旋转方式的不同。
|
|
|
+> 小鱼说:无论是参考自身坐标系还是参考固定的坐标系,都有12种旋转方式,所以欧拉角有12*2=24种旋转方式,后面的计算中我们也将直观的感受到24种旋转方式的不同。
|
|
|
|
|
|
### 2.3 固定转轴欧拉角 转 旋转矩阵
|
|
|
首先我们来考虑绕固定的坐标系旋转如何转换成旋转矩阵
|
|
|
|
|
|
-我们以顺序XYZ来举例说明,其他旋转顺序类似
|
|
|
+我们以XYZ的旋转顺序来举例说明,其他旋转顺序类似
|
|
|
|
|
|
现在假设A、B两个坐标系重合,B坐标系绕A坐标系的X轴旋转45度,绕A的Z轴旋转90度.
|
|
|
|
|
|
@@ -187,7 +187,7 @@ $$
|
|
|
|
|
|
这里引用林沛群老师的解释:
|
|
|
|
|
|
-我们可以假设一个向量v固定在B坐标系上,那我们让B坐标系绕着A坐标系的三个轴做旋转,就可以认为是让向量v绕着坐标系A的三个轴做旋转,那先转的肯定先乘,所以我们先让向量v乘上Rx(45),再让其乘上Rz(90),即:
|
|
|
+我们可以假设一个向量v固定在B坐标系上,那我们让B坐标系绕着A坐标系的三个轴做旋转,就可以认为是让向量v绕着坐标系A的三个轴做旋转,那先转的肯定先乘,所以我们先让向量v乘上Rx(45),再让其乘上Rz(90),即:
|
|
|
$$
|
|
|
v' = R_{Z(90)}(R_{X(45)}v)
|
|
|
$$
|
|
|
@@ -203,7 +203,7 @@ $$
|
|
|
最终结果:
|
|
|
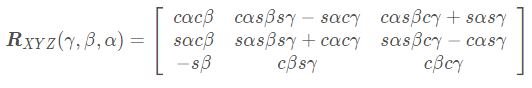
|
|
|
|
|
|
-根据旋转顺序不同,固定角有12种旋转方式,这里我们给出了绕固定轴以XYZ顺序旋转欧拉角转旋转矩阵的等式,其他旋转顺序对应的旋转矩阵可以尝试自行推导.
|
|
|
+根据旋转顺序不同,固定角有12种旋转方式,这里我们给出了绕固定轴以XYZ顺序旋转欧拉角的转旋转矩阵的等式,其他旋转顺序对应的旋转矩阵可以尝试自行推导。
|
|
|
|
|
|
### 2.2 非固定旋转轴的欧拉角
|
|
|
|
|
|
@@ -241,11 +241,11 @@ $$
|
|
|
说到这里相信你已经理解了轴角的意义,接着我们给出轴角和旋转矩阵之间的转换关系
|
|
|
|
|
|
### 轴角转旋转矩阵
|
|
|
-假设坐标系B和参考坐标系A宠儿,将B绕着A坐标系下的矢量$^AK$按右手定则旋转$\theta$角度,旋转之后B坐标系在A坐标系下的姿态可以用
|
|
|
+假设坐标系B和参考坐标系A重合,将B绕着A坐标系下的矢量$^AK$按右手定则旋转$\theta$角度,旋转之后B坐标系在A坐标系下的姿态可以用
|
|
|
$$
|
|
|
^A_BR(K,\theta)
|
|
|
$$
|
|
|
-表示,注意矢量K为单位矢量(模场为1),K为一个3*1的矢量
|
|
|
+表示,注意矢量K为单位矢量(模长为1),K为一个3*1的矢量
|
|
|
$$
|
|
|
^AK=[k_x,k_y,k_z]^T
|
|
|
$$
|
|
|
@@ -272,7 +272,7 @@ $\theta$的符号由右手定则确定,右手大拇指指向矢量K的方向.
|
|
|
|
|
|
## 4.四元数
|
|
|
|
|
|
-除了轴角可以使用一个表示角度和三个表示旋转轴,一共四个数字表示旋转外。还有另外一种方式可以表示旋转——四元数。
|
|
|
+除了轴角可以使用一个数字表示角度,三个数字表示旋转轴,一共四个数字表示旋转外。还有另外一种四个数字表示表示旋转的方式——四元数。
|
|
|
|
|
|
四元数的四个数字由一个实部和三个虚部组成,是一个超复数形式
|
|
|
|
|
|
@@ -283,7 +283,7 @@ $$
|
|
|
|
|
|
关于四元数的由来有个小故事,小鱼分享一下:
|
|
|
|
|
|
-> 1843年10月16日的傍晚,英国数学家哈密顿和他的妻子一起步行去都柏林,途中经过布鲁哈姆桥时,他的脚步突然放慢了。妻子以为他要尽情欣赏周围的景色,于是也放慢了脚步。其实哈密顿此时正在思考他久久不能解决的问题。早在1828年,他就想发明一种新的代数,用来描述绕空间一定轴转动并同时进行伸缩的向量的运动。他设想这种新代数应包含四个分量:两个来固定转动轴,一个来规定转动角度,第四个来规定向量的伸缩。但是在构造新代数的过程中,由于他受传统观念的影响,不肯放弃乘法交换律,故屡受挫折。哈密顿盲目地相信,普通代数最重要的规律必定继续存在于他寻找的代数中。然而此刻,他的脑际突然产生了一个闪念:在所寻找的代数中,能否让交换律不成立呢?比方说,A×B不等于B×A而是等于负的B×A。这个想法太大胆了,他感到非常激动。哈密顿马上掏出笔记本,把他的思想火花记录下来。这一火花就是I,J,K之间的基本方程,即四元数乘法基本公式。哈密顿因此把1843年10月16日称为四元数的生日。此后,哈密顿一生的最后22年几乎完全致力于四元数的研究,成果发表在他去世后出版的《四元数基础》一书中。四元数的出现,推倒了传统代数的关卡,故有数学史上星程碑的美誉。后人为了纪念这一发明,特意在当年哈密顿刻划过的石头上镶嵌了一块水泥板,上面清楚地记载着1843年曾经发生的故事。
|
|
|
+> 1843年10月16日的傍晚,英国数学家哈密顿和他的妻子一起步行去都柏林,途中经过布鲁哈姆桥时,他的脚步突然放慢了。妻子以为他要尽情欣赏周围的景色,于是也放慢了脚步。其实哈密顿此时正在思考他久久不能解决的问题。早在1828年,他就想发明一种新的代数,用来描述绕空间一定轴转动并同时进行伸缩的向量的运动。他设想这种新代数应包含四个分量:两个来固定转动轴,一个来规定转动角度,第四个来规定向量的伸缩。但是在构造新代数的过程中,由于他受传统观念的影响,不肯放弃乘法交换律,故屡受挫折。哈密顿盲目地相信,普通代数最重要的规律必定继续存在于他寻找的代数中。然而此刻,他的脑际突然产生了一个闪念:在所寻找的代数中,能否让交换律不成立呢?比方说,A×B不等于B×A而是等于负的B×A。这个想法太大胆了,他感到非常激动。哈密顿马上掏出笔记本,把他的思想火花记录下来。这一火花就是I,J,K之间的基本方程,即四元数乘法基本公式。哈密顿因此把1843年10月16日称为四元数的生日。此后,哈密顿一生的最后22年几乎完全致力于四元数的研究,成果发表在他去世后出版的《四元数基础》一书中。四元数的出现,推倒了传统代数的关卡,故有数学史上里程碑的美誉。后人为了纪念这一发明,特意在当年哈密顿刻划过的石头上镶嵌了一块水泥板,上面清楚地记载着1843年曾经发生的故事。
|
|
|
|
|
|
|
|
|
|
|
|
@@ -311,7 +311,7 @@ $$
|
|
|
|
|
|

|
|
|
|
|
|
-四元数转轴角
|
|
|
+轴角转四元数
|
|
|
|
|
|
轴:$^AK=[k_x,k_y,k_z]^T$ 角:$\theta$
|
|
|
$$
|